# 2025년 2월 10일 종이책 3쇄 정오표
* 종이책 1쇄, 2쇄와 전자책 3.0 이전 버전을 구입하신 독자분들도 확인하시기 바랍니다.
p45. 위에서 5째 줄
● CMake 다운로드 주소: https://cmake.org/download/
이 책을 쓰는 시점에서 CMake의 최신 버전은 3.22.1이며, 책의 모든 예제는 3.1x 버전 이상이면 동작이 가능하도록 제작됐다. 자신의 운영체제에 맞는 인스톨러 파일을 내려받고 설치를 진행한다.
→
단, 이 책을 집필한 시점에서 CMake의 최신 버전은 3.22.1로서, 책의 모든 예제를 안전하게 실행하기 위해서는 동일한 3.22.1 버전을 사용할 것을 권장한다.
● CMake 3.22.1 다운로드 주소: https://cmake.org/files/v3.22/cmake-3.22.1-windows-x86_64.msi
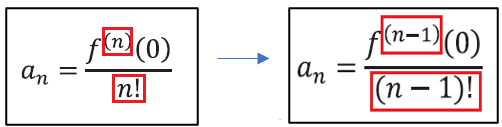
p546. 본문 맨 아래 수식

# 2022년 10월 10일 종이책 2쇄 정오표
* 종이책 1쇄와 전자책 3.0 이전 버전을 구입하신 독자분들도 확인하시기 바랍니다.
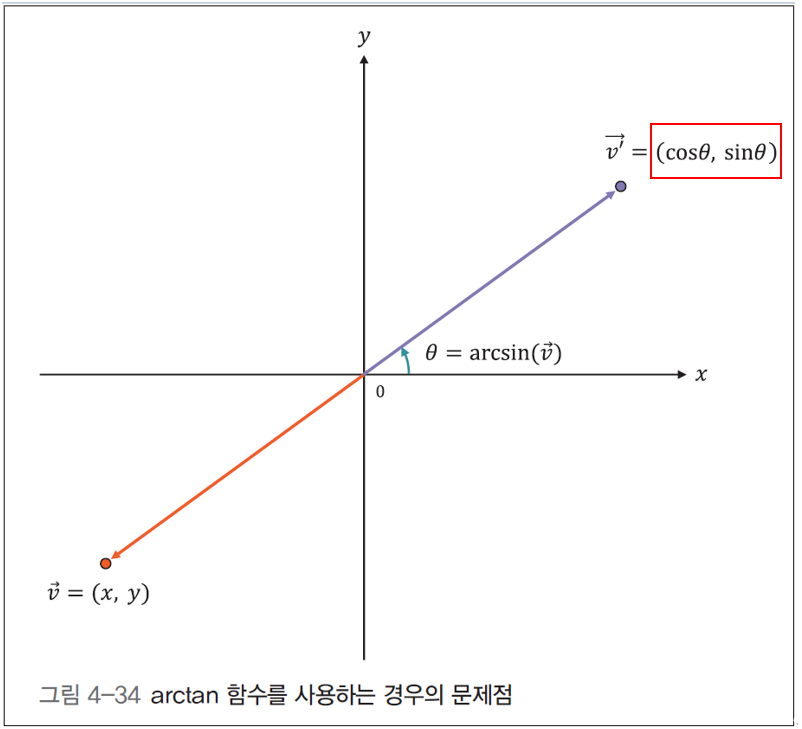
p145. 그림 4-34 1사분면
(sinθ, cosθ) → (cosθ, sinθ)
p145. 밑에서 2째 줄
각의 크기를 x축으로 둔 → 각의 크기를 y축으로 둔
p160. 밑에서 5째 줄 (마지막 수식) (전자책 v3.0에는 모두 수정/반영된 사항입니다)
cosθ x + sinθ y
→ sinθ x + cosθ y
p160. 밑에서 4째 줄 (전자책 v3.0에는 모두 수정/반영된 사항입니다)
c = cosθ, d = sinθ
→ c = sinθ, d = cosθ
p227. 본문 17번 설명 오타
스크린 좌표예 → 스크린 좌표에
p361. 본문 9~10째줄 오일러각 데이터 오류 (전자책 v3.0에는 모두 수정/반영된 사항입니다)
(α, 0, 0) → (0, α, 0)
(β, 0, 0) → (0, β, 0)
p476. 코드부 7~11째 줄(리스트13-8) (전자책 v3.0에는 모두 수정/반영된 사항입니다)

→

p476. 17째 줄 (전자책 v3.0에는 모두 수정/반영된 사항입니다)
➍ 중점으로부터 모든 점의 거리를 구하고 이 중에서 가장 큰 값을 반지름으로 지정한다.
→
➍ 중점에서 거리가 가장 먼 점의 위치를 구하고, 이 점과 중점 사이의 거리를 반지름으로 지정한다.
p535. 수식 4째 줄 수식 수정

→

p540. 식 15-11 설명 5째 줄 내용 수정

→

p548. 식 15-15 수정
p550. 마지막 수식, cos 함수의 매클로린 급수 전개식 수정

→

p560. 본문 위에서 2째 줄
곱셈에 대해 결합법칙이 성립하지 않는다
→
곱셈에 대해 교환법칙이 성립하지 않는다
# 2022년 6월 24일 전자책 v2.0 정오표
* 종이책 1쇄와 전자책 v1.0을 구입하신 독자분들도 확인하시기 바랍니다.
p211. 식6-1
ax₁ + ax₂
→ ax₁ + bx₂
p261. 17째 줄 (8번 원문자 있는 줄) 밑에 다음 행 추가
r.DrawLine(lineStart, point, LinearColor::Red);
p272. 예제 8-1 밑에서 6째줄
}; (4)
→ };
p370. 그림11-4 수식
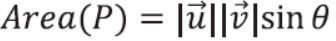

p459. 본문 11~12째 줄

p464. 코드 19~22째 줄
Plane(Vector3(pCos, 0.f, pSin), 0.f), // +X
Plane(Vector3(-pCos, 0.f, pSin), 0.f), // -X
Plane(Vector3(0.f, pCos, pSin), 0.f), // +Y
Plane(Vector3(0.f, -pCos, pSin), 0.f), // -Y
→
Plane(Vector3(pCos, 0.f, pSin), 0.f), // +Y
Plane(Vector3(-pCos, 0.f, pSin), 0.f), // -Y
Plane(Vector3(0.f, pCos, pSin), 0.f), // +X
Plane(Vector3(0.f, -pCos, pSin), 0.f), // -X
p536. 수식 제외하고 밑에서 4째줄
좌변의 극한식은
→ 우변의 극한식은
p540. 식 15-11의 유도 과정 2번째 행의 분자
cos²θ - 1
→ cos²h - 1
p568. 밑에서 5번째 줄 (식 유도 과정 2번째 행)
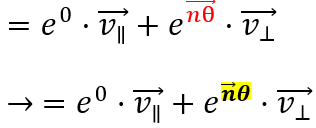
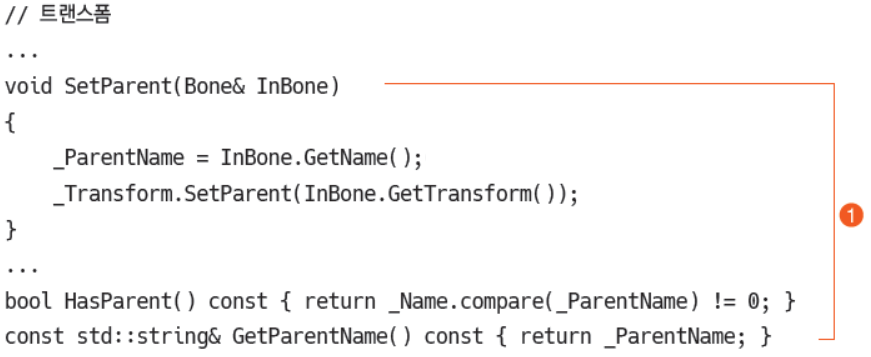
p629. 리스트 17-14 //트랜스폼 이후
코드 끝의 (1)을 삭제하고 해당 부분을 모두 묶어서 ①로.

→
# 2022년 2월 22일 종이책 1쇄 / 2022년 4월 25일 전자책 v1.0 정오표
p21 / p521. 14.2.1 절번호 수정
14.2.1 켤레 복소수의 회전 변환
→ 14.2.2 켤레 복소수의 회전 변환
p99. 본문 밑에서 2째 줄
그림 3-16과 같이 원점과 벡터를 연결해
→ 그림 3-17과 같이 원점과 벡터를 연결해
p104. 예제 3-2 중 ⓫주석의 코드부
r.DrawPoint(v + center, LinearColor : : Red);
→ r.DrawPoint(v + currentPosition, LinearColor: : Red);
p120. 그림 4-9 제목 -> sin 함수(b)와 cos 함수(a) 그래프
p123. 본문 9째 줄 / 그림 4-14에서 1rad(라디안) 값 오류
52.2958 -> 57.2958
p160. 본문 9째 줄, "1차 동시성" 설명부 수식 오류

-> 가법성에 관한 수식이므로 다음의 1차 동시성 수식으로 바로잡습니다.
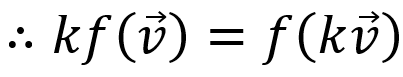
p160. 본문 밑에서 7째 줄, 식 설명 중 c와 d 대입값 오류
이는 (ax + by, cx + dy)의 형식에 a = k, b = 0, c = k, d = 0를 대입한 결과와
→ 이는 (ax + by, cx + dy)의 형식에 a = k, b = 0, c = 0, d = k를 대입한 결과와
p173. [참고] 박스 설명 중
2째 줄 : 시계 방향으로 90°로 회전한 → 시계 반대 방향으로 90°로 회전한
4째 줄 : 시계 반대 방향으로 90°로 회전한 → 시계 방향으로 90°로 회전한
p175. 위에서 1째 줄
1행 1열에 → 1행 2열에
p179. ➍번, ➎번 코드행 오류
trasnformedV → transformedV
p180. 아래에서 두 번째 줄
항등행렬 Identity atrix → 항등행렬Identity matrix
p184. 아래에서 두 번째 줄
크게 변환에 → 크기 변환에
p238. 표 7-1 삼각형 변을 구성하는 벡터
c = A - B = (|c|cosβ, |c|sinβ, 0) → c = A - B = (|c|cosβ, |c|sinβ)
b = C - A = (|a| - |c|cosβ, 0 - |c|sinβ, 0) → b = C - A = (|a| - |c|cosβ, 0 - |c|sinβ)
p242. 위에서 5째 줄
5.4.5절에서 → 5.4.4절에서
p278. 예제 8-2 중 4번째 주석 문구
// 공통 분모 ( uu * vv - uv * uv ) → // 공통 분모 ( uv * uv - uu * vv )
p540. 식 15-11의 유도 과정 중 2번째 설명부 <삼각함수 기본공식> 오류
분자에 삼각함수 공식 (cosθ)^2 + (cosθ)^2 = 1을 적용해
→ 분자에 삼각함수 공식 (cosθ)^2 +(sinθ)^2 = 1을 적용해
p620. 식 17-2 수정

→

X, Y, Z의 아랫첨자 변경, *s이 괄호 안으로 들어감
p620. 리스트17-10 마지막 줄 (③행)
result.SetPosition(InParentWorldTransform.GetPosition() + InParentWorldTransform. GetScale() * (InParentWorldTransform.GetRotation() * GetPosition()));
→ result.SetPosition(InParentWorldTransform.GetPosition() + InParentWorldTransform.
GetRotation() * (InParentWorldTransform.GetScale() * GetPosition()));
p624. 식 17-6 수정

→
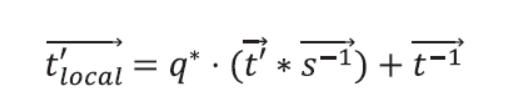
(q·t)*s → q·(t*s) 로 괄호 위치 변경됨.
p624. 리스트17-12 9째 줄 (④행)
result.SetPosition(invParent.GetPosition() + invParent.GetScale() * (invParent.GetRotation() * GetPosition()));
→ result.SetPosition(invParent.GetPosition() + invParent.GetRotation() * (invParent.GetScale() * GetPosition()));
'+ 도서 오류 정보' 카테고리의 다른 글
| [정오표] 코틀린 쿡북 (0) | 2022.04.25 |
|---|---|
| [정오표] UX/UI의 10가지 심리학 법칙 (0) | 2022.03.28 |
| [정오표] 실전 카프카 개발부터 운영까지 (13) | 2021.11.01 |
| [정오표] 엘라스틱 스택 개발부터 운영까지 (2) | 2021.08.24 |
| [정오표] 스프링 부트 실전 활용 마스터 (0) | 2021.06.10 |

댓글